There is often much confusion over the meaning of ‘enzyme units’, ‘enzyme activity’ and ‘specific enzyme activity’. This guide explains these key concepts in simple terms and discusses enzyme assay design and the importance of operating in the ‘linear range’. We also consider standard curves and whether you should plot concentration or absolute amount of product on the x axis. Some tips on setting up assay controls and subtracting blanks are discussed. Finally, we explain how enzyme activity values are calculated and we give a simple overview of kinetic equations.
Definitions of Enzyme Units
Enzymology would be less complicated if everyone used the same unit definition. A standard unit definition is given below:
1 unit (U) is the amount of enzyme that catalyses the reaction of 1 µmol of substrate per minute (definition A).
In most R&D settings, 1 umol of substrate is actually quite a lot of material and other definitions may be preferred to avoid expressing quantities in fractions of units. The following non-standard definition is commonly used:
1 unit (U) is the amount of enzyme that catalyses the reaction of 1 nmol of substrate per minute (definition B).
Note that the change in definition has a profound effect on the stated number of units i.e. 1 unit of enzyme according to definition A would equate to 1000 units according to definition B!
You may also see enzyme units expressed as milli-unit (or mU) which simply means a thousandth of a unit, irrespective of how the unit has been defined.
Clearly the actual amount of an enzyme in a tube is not altered simply by changing the unit definition, but care is required when comparing the activities of samples from different suppliers. As long as the unit definitions are provided you can transform the stated number of units into nmol per min, which is unambiguous and allows valid comparisons to be made.
For clarity in your own work you may prefer to use ‘nmol per min’ (or ‘µmol per min’), though if constant repetition is required then clearly the much shorter term ‘unit’ has its attractions.
What Is ‘Enzyme Activity’?
Activity is quoted in units per ml (U/ml), in other words nmol per min per ml (if unit definition B has been adopted). Thus activity values expressed in units are also subject to an illusory 1000-fold ‘increase’ if one switches from unit definition A to unit definition B. Again there cannot be any confusion if activity is expressed in terms of nmol per min per ml rather than units per ml.
Since activity relates to concentration it follows that two vials of enzyme can contain the same number of units (in total) but have different activities (concentrations).
What Is Specific Enzyme Activity?
Specific enzyme activity (usually stated simply as ‘specific activity’) is the number of enzyme units per ml divided by the concentration of protein in mg/ml. Specific activity values are therefore quoted as units/mg or nmol/min/mg (if unit definition B is applied).
Specific activity is an important measure of enzyme purity and values for different batches of a pure enzyme should be the same, within normal experimental error.
Serial dilutions of an enzyme solution will have different enzyme activity values, but identical specific activity values because in calculating specific activity the numerator (units/ml) and denominator (mg/ml) are affected equally by sample dilution.
Although specific activity is very different from activity, the calculation of specific activity nonetheless is dependent on the activity value, and therefore the stated specific activity value will also be dependent on the enzyme unit definition. Batches that are below the expected specific activity value may contain impurities or enzyme molecules that have become denatured.
Factors Affecting Enzyme Activity
In this section we discuss why one enzyme may have different measured activity values in different labs. By this we mean real differences in measured activity, not apparent differences caused by the use of different unit definitions.
The conditions under which an assay is carried out will influence the reported activity values. For example, assays typically are carried out at a temperature between 20-37°C. Generally speaking, an enzyme will be more active at 37°C than at 20°C.
The definition of the enzyme unit would be better expressed thus:
1 unit (U) is the amount if enzyme that catalyses the reaction of 1 nmol of substrate per minute under standard conditions.
Unfortunately, the term ‘standard conditions’ is open to interpretation and there may be different user preferences, at least in R&D environments. Thus ten different research labs may (quite correctly) calculate different activities for the same solution of enzyme. Most research labs establish their own ‘standard conditions’ and check each new batch internally. In clinical settings ‘standard conditions’ are explicitly defined and all labs are required to run identical assays.
Developing Assays and the Importance of Linear Range
The activity value (units/ml) for your enzyme is the most important parameter when you are developing an assay. This is because the volume (i.e. number of units) that you add will determine the amount of substrate that is converted into product. Remember, 1 unit catalyses the conversion of 1 nmol of substrate per min (definition B).
The reported units/ml may give you a rough idea of how much enzyme to add, but as the activity value may not have been determined in a test identical to yours, it is usual to prepare serial dilutions of the enzyme (e.g. log dilutions initially) and to test a fixed volume of each dilution. Depending on the assay signal (which will be related to the amount of substrate converted) a second experiment may be required to home in on a suitable dilution.
What exactly is the ‘best’ dilution? To answer this, we need to think about the most important aspect of assay design - linear range. It is important for quantitative work to operate in a range in which a plot of assay signal (often absorbance) versus enzyme concentration is linear. Most assays are linear if the degree of substrate conversion is less than 15%, assuming that there are no other limiting factors. By fixing the assay time (e.g. 30 min) and temperature (e.g. 25°C) the degree of conversion can be controlled simply by adjusting one parameter i.e. the number of enzyme units added.
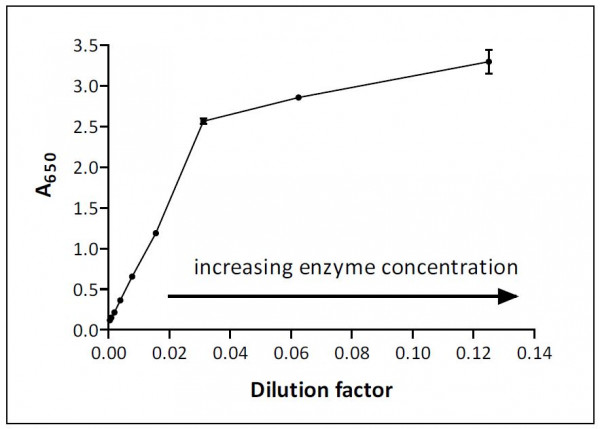
This is illustrated graphically in Figure 1 with dilutions expressed as reciprocals (i.e. dilution of 1/10 = 0.1 on the x axis). Your own plot may differ in its shape and linear range but at very high enzyme concentration undoubtedly the assay signal will not increase in proportion to the amount of enzyme added.
The assay in Figure 1 is linear up to optical density (OD) 2.5 and a dilution factor of 0.02 (1/50 dilution of enzyme) would be ideal for assay work, as it gives a large signal (~1.5) and lies in the middle of the linear range. Calculations based on results for dilution factors in the range between 0.04 and 0.12 (i.e. the region with reduced slope) will underestimate the true level of enzyme activity because something is clearly limiting the magnitude of the assay signal.
Many factors may operate to limit the linear range and the range will vary from assay to assay. One common reason for non-linearity is excessive consumption of substrate, which can cause the rate of reaction to fall, but limitations of the optical components of the plate reader (or whatever measuring device is used) may also be significant. Most plate readers for example cannot reliably measure absorbance values above 3 and this limitation will apply regardless of the percentage of the substrate that has been converted into product.

Fig. 1: Absorbance Versus Amount of Enzyme
Although not otherwise discussed in this guide, one should also be aware that enzymes can denature over time (especially if they are very dilute) and the products of some reactions can inhibit the enzyme. Indeed there are other possible reasons for non-linear behaviour but it is usually relatively easy to find the linear range by trial and error using serial dilutions of the enzyme as described above.
Assay Time and Temperature
These parameters can also influence the linear range as they affect the rate of substrate conversion. For example, an assay may be linear after 15 min, but at 60 minutes too much substrate may have been consumed. In this situation you would have to reduce the amount of enzyme in order to run your assay for 60 minutes. The same considerations apply to assay temperature as it can also affect the rate of reaction.
Most people adopt an assay time of somewhere between 15 min and 60 min. Very short times (e.g. 2 min) are to be avoided because a slight delay in stopping the reaction will lead to a significant error in calculations of activity. It is important to ensure that reagents stored in a fridge or freezer have equilibrated to the correct temperature before use, and this is especially important if you have a relatively short assay time.
Assay Volume/Sensitivity
From a practical perspective the assay volume is determined/limited by the consumable item that you use for your assays (e.g. cuvettes, tubes, or microplates). The signal for most enzyme assays is proportional to the assay volume and attempts to miniaturise the assay (e.g. to conserve reagents) will usually lead to lower signals. However, absorbance assays are often an exception, and a switch from a 3 ml cuvette to 1 ml micro-cuvette, for example, will not change the absorbance reading if the width (path length) of the cuvette is still 1 cm (i.e. the light still passes through the same ‘length’ of liquid). This is because absorbance is proportional to path length, not to the volume of sample.
In microplate absorbance assays, the path length is equal to the depth of the liquid, and it is possible to miniaturise without loss of signal by reducing the diameter of the wells and maintaining a constant depth of liquid. For example, 96 well plates can easily accommodate 200 µl of sample, but with a 50 µl assay volume it would be better to use a 384-well plate to increase the path length over that seen with 50 µl of sample in a 96-well plate.
Continuous Assays (Measuring Product Appearance over Time)
Most assays are carried out for a fixed period time (end point assays) and the reaction is halted by the addition of a stop reagent (e.g. acid). However, in continuous assays the appearance of product (less commonly the consumption of substrate) is recorded continuously (e.g. by means of a chart recorder). The same basic rules apply; a plot of signal versus time for a fixed amount of enzyme should be linear and the rate should double if the amount of enzyme is doubled. As long as the assay is being operated in the linear range, the activity of appropriately diluted ‘unknowns’ can be accurately determined from the initial rates of reaction measured with a set of standards.
What Substrate Concentration Should I Use?
The concentration of substrate will influence the rate of reaction but there are several factors to consider in selecting the ‘right’ concentration. From a practical point of view one key consideration is the amount of product that must be generated in order to give a measurable assay signal. Since the rate of an enzyme reaction is likely to fall when more than about 15% of the substrate has been hydrolysed, the initial concentration of substrate should generally be at least 10x the concentration of product that is known to give an acceptable assay signal.
Another consideration is the Km for the substrate. While adding more substrate generally means that you will see higher activity values, the relationship is not linear and the cost of the substrate may need to be considered. At this point it is probably useful to introduce the classic Michaelis-Menten equation:
v = (vmax S)/(Km + S) ................ Equation (1)
where v is the rate, vmax is the maximum possible rate, S is substrate concentration and Km is equal to the substrate concentration that gives half maximal activity. The derivation of this equation and its underlying assumptions may be found in any text book on enzyme kinetics. Although it is normal to measure rather than to calculate the rate of enzyme reactions, it is useful to understand the underlying principles for the purpose of assay design.
The Michaelis-Menten equation is useful in that it helps you to select a suitable concentration of substrate if the Km is known.
When S=Km, v = (vmax S)/2S, i.e. v/vmax = S/2S = ½.
In other words, the enzyme will be operating at 50% of it maximum possible rate when S=Km. By substituting into equation (1) the values for S = 10 and Km = 1 you will see that by increasing the substrate concentration 10-fold the enzyme now works at ~90% of it maximum possible rate, instead of 50%. Clearly this is higher, but not 10 times higher. At very high concentrations of substrate the Km in equation (1) numerically becomes insignificant and the measured rate then equals vmax.
Many assays are run with substrate concentration at or around the Km value but if the Km is very high it may not be possible to use such a high concentration of substrate (e.g. for reasons of cost or limited solubility). In some situations it may be even advisable to use a relatively low concentration of substrate. For example, in pharmaceutical drug discovery, the use of a very high substrate concentrations would make it more difficult to identify competitive enzyme inhibitors (competitive inhibitors bind to the same site as the substrate). A balance of the various factors has to be struck so that the assay has a measurable signal, can be operated in the linear range and can meet any other assay objectives (e.g. cost, time and so on).
Standard Curves
A standard curve is always required if you wish to calculate enzyme activity. It is not essential if you are only interested in relative activity values. The standard curve is constructed by measuring the assay signal with standard solutions of the reaction product over a suitable range of concentrations. Ideally you should run a standard curve for every experiment, but if the standard curve is highly reproducible it may be acceptable to run it periodically.
A typical standard curve is shown in Figure 2 below. This is a standard curve for an ATPase assay, in which ATP is hydrolysed to ADP and Pi (inorganic phosphate).

Fig. 2: Standard Curve for Pi
The phosphate is detected by means of a dye binding reagent which changes colour in the presence of phosphate. However, the specifics of this test are not important here; whatever the nature of the product or the method of detection that is used, a standard curve showing the dependence of signal on the amount of product in the assay must be constructed. The ‘curve’ (ideally it is a straight line) is used to determine the amount of product generated in samples with unknown activity i.e. from the absorbance value, by reading off the intercept on the x- axis (most graphical software packages will automatically calculate values of x from measured values of y). The amount of activity can then be calculated (see later).
Do I Plot Concentration or Absolute Amount on the X Axis?
There is no single correct answer here, and the possibility of using either approach can often cause confusion when activity values are calculated. For example, plotting nmol of product on the x axis is very convenient if you need to calculate activity values (remember, activity = nmol per min per ml). However, laboratory reagents are usually prepared at known concentrations, and it is often easier to plot these values on the x axis. However, when you calculate the activity (or specific activity) of your enzyme you must remember to convert the concentration on the x-axis into the number of nmoles of product formed, which means you must take account of the assay volume. The reason is easy to understand: 50 µl and 100 µl volumes of a standard solution will be at the same concentration, but the larger volume will contain twice the amount of product. Generally, it is best to pick one approach (i.e. either plot absolute amount of product or concentration) so that the same method calculating activity is always used.
Controls and Subtraction of ‘Blank’ Data
Proper controls are vitally important for quantitative work, as is the correct use of the control data in calculations. Controls tell you (indirectly) how much of the assay signal is due to the action of the enzyme and how much arises for other reasons. A common source of ‘false’ signal is the substrate (which may often be contaminated with product). Other assay components may also give rise to a small signal depending on the nature of the components and the type of assay. The purpose of controls is to allow you to remove (by subtraction) any elements of the total signal that are not related to the action of the enzyme. If the assay is well-designed and the assay reagents are of good quality the treatment of controls is usually quite simple.
Some general guidelines are given below:
If we return to the colorimetric assay for detecting inorganic phosphate (Pi) we can highlight some potential problems that are readily detected with proper controls. The phosphate detection reagent gives a low reading of about 0.08 in a 96- well plate at the wavelength used for measurement (around 650nm). We might set up the following assays/controls (readings in parentheses in a hypothetical assay situation):
- All assay components minus enzyme (0.5)
- Enzyme on it own (0.1)
- Enzyme plus all other components (1.8)
Clearly the assay signal of 1.8 is not due solely to the action of the enzyme on the substrate. For any enzyme assay, a key control (A) is to leave out the enzyme (and replace with buffer). This will give you the background signal for all the other assay components as a group, including the substrate which may contain a small amount of product. This control does not tell you the background signal for the enzyme, but clearly you cannot add the enzyme to the substrate as a control! In most assays the enzyme gives no signal because it is diluted down significantly before use in assay. This can easily be checked, as in B above.
The data for sample A suggest that the mixture is contaminated with inorganic phosphate. The individual components can then be checked to identify the source of the problem. This situation is quite common for assays of ATPases and other phosphate- generating enzymes, as the substrates are often unstable and are partially hydrolysed to give some inorganic phosphate.
It can be awkward to correct raw data if several components give false signals; elimination of the problem at source is generally far better than any mathematical treatment. The ‘corrected’ value for sample C above may appear to be 1.2 (i.e. 1.8 - 0.5 - 0.1) but strictly speaking this is wrong. Remember the assay plate plus detection reagent give a background signal of around 0.08, so the source of most of the signal for control A is the plastic of the plate and/or the detection reagent. The same small signal must also be hidden within the value for the enzyme control. Thus in the correction applied above we have subtracted this hidden blank twice.
You will always need to subtract controls from assay data, and it is preferable to combine all substances (except enzyme) and subtract a single value. If this approach is taken, the standard curve is treated in the same way and a control value is subtracted (i.e. the value obtained in the absence of product, i.e. analogous to the plate/reagent blank discussed above). Thus neither the subtracted assay data nor the subtracted standard curve contains the potentially misleading background signal caused by the plate/assay reagent.
Finally, as we have seen, false signals are easily detected with proper controls but the best strategy to get good quality data is to use reagents with low backgrounds so that the controls values are low. It is also useful to generate an assay signal (due to enzyme) that is far higher than any background signal. Ideally the signal-to-background ratio should be at least 5 and preferably 10 or more for accurate quantitative work.
Calculating Activity Values
This is fairly easy to understand if we back-calculate from raw assay data in step-wise fashion. For example, let us say we have generated 10 nmol of product in our enzyme reaction (i.e. determined from the standard curve of signal versus absolute amount of product). Since activity is expressed as nmol per min per ml, we need to consider time and volume and, perhaps less obviously, the amount and dilution of enzyme in order to calculate activity.
If the assay is 10 min long, the number of nmol per min in the example above is 1. (Step 1)
If the assay volume is 200 µl, we need to multiply by 5 (i.e. 1000/200) to get nmol per min per ml. (Step 2)
This value relates to the activity of the enzyme in the assay, not in the sample of enzyme used to set up the assay. Some further corrections factors are needed to determine the enzyme activity in the original sample of enzyme.
The enzyme may have been diluted before use, and it has to be further diluted by the other components present in the assay. If the assay (200 µl in total) comprises 20 µl of enzyme, and the enzyme is pre-diluted 1/100 before the 20 µl sample is added, you can probably see that we should multiply first by 10 (step 3) and then by 100 (step 4) to get the activity of the enzyme in the original enzyme solution.
So far this is relatively straightforward. However, we mentioned earlier that concentration is often plotted on the x axis of the standard curve. Thus the values might be expressed in mM terms (not mmol) and you cannot determine the number of mmol simply by inspecting the standard curve.
Since mM means mmoles per litre, we have a discrepancy between the implied volume of 1L and the actual assay volume. Thus if we have 10mM product and the assay volume is 200ul, we need to divide by 5000 to get the number of mmoles of product.
You may notice here that dividing by 5000 here offsets some of the multiplication operations that were required above. Indeed, it is quite normal for correction factors to cancel out. For example, in a 10 minute assay using 1/10 diluted enzyme, you will divide by 10 to get nmol per min and multiply by 10 later on to correct for the dilution factor.
It follows that if you always use standard assay conditions (i.e. your standard), you will be able to multiply the ‘x’ value from standard curve by a single global correction factor, which encompasses all of the other individual correction factors, to calculate your activity values. Only on the first occasion do you need to identify the individual correction factors.
Enzyme Inhibition/Drug Screening
This is an area of enzymology where there remains a need to operate in the linear range but where calculations of activity values are not usually relevant; rather the relative rate of reaction (or relative amount of product formed) in the presence and absence of a test substance is key, which requires little more than simple calculations using the blank- subtracted assay data. After subtraction of the blanks, the amount of product formed is expressed as a percentage of the amount obtained in the absence of the test substance (i.e. 100%). These assays can sometimes be run with quite low signal-to-background ratios, because the question being asked ("Does the test substance inhibit the reaction?") only requires a yes/no answer.
Summary
This guide hopefully has provided clear explanations of ‘enzyme units’, ‘enzyme activity’ and ‘specific enzyme activity’, and unit definitions and the importance of the ‘linear range’. The specifics of what to plot on the x-axis of standard curves is a matter of user preference but some care is required when activities are calculated. Assay controls are important but using high quality reagents is better than removing backgrounds using mathematical approaches. A high signal to background ratio is desirable for quantitative work and a number of parameters can be varied to increase the assay signal; it is not always necessary simply to add more enzyme. Enzyme activity values can be calculated easily if a stepwise approach is used to identify the key assay variables.